Análise detalhada do circuito da série RC
2024-05-08
20474
O circuito da série RC, composto por um resistor e um capacitor, serve como um componente fundamental nos projetos básicos e avançados de sistemas eletrônicos.Ajuda a entender os principais princípios, como resposta de frequência, mudança de fase e filtragem de sinais, que desempenham um papel significativo no projeto do circuito e no processamento de sinais.Essa exploração abrange o básico teórico e se estende a aplicações práticas por meio de experimentos e simulações.Ao montar fisicamente o circuito ou modelá -lo digitalmente, os alunos podem entender visualmente o processo de carregamento e os efeitos dos íons V ariat do componente, tornando os conceitos complexos mais acessíveis e memoráveis.
Catálogo

Figura 1: Diferentes tensões de saída dos circuitos RC
Introdução ao circuito RC
Um circuito RC, abreviado para o circuito de capacitância de resistência, é fundamental em eletrônicos para manipular sinais através de resistores e capacitores.Esses circuitos são particularmente conhecidos por sua capacidade de mudar fases e filtrar sinais, usando arranjos simples desses componentes.Um circuito RC básico, geralmente chamado de circuito RC de primeira ordem, geralmente inclui apenas um resistor e um capacitor.
Em uma configuração típica, a tensão de entrada é aplicada ao arranjo em série de um resistor e um capacitor.A saída pode ser desenhada através do resistor ou do capacitor, cada uma dando respostas diferentes às frequências de sinal devido às características únicas do capacitor.Essa versatilidade permite que os circuitos RC desempenhem uma variedade de funções em dispositivos eletrônicos, como sinais de acoplamento e filtragem ou até mesmo conversão de formas de onda quando submetidos a uma tensão de etapa.
O circuito RC pode ser configurado de várias maneiras-séries, paralelas ou uma combinação de ambos, conhecida como paralela em série.Cada configuração afeta as frequências de sinal de maneira diferente: as conexões em série tendem a atenuar as baixas frequências, enquanto as conexões paralelas são usadas para atenuar as frequências mais altas.Essa diferença se deve principalmente à maneira como os resistores e capacitores interagem com o circuito;Os resistores se opõem diretamente à corrente enquanto os capacitores o armazenam e o liberam, impactando como o circuito responde a diferentes frequências.
Ao contrário dos circuitos que incluem indutores, como os circuitos LC, os circuitos RC simples não podem ressoar, pois os resistores não armazenam energia.Esse atributo influencia claramente como os circuitos RC são utilizados, concentrando -se em sua capacidade de filtrar, em vez de armazenamento ou ressonância de energia.Cada configuração serve a um objetivo específico, tornando as ferramentas versáteis dos circuitos RC em estudo teórico e aplicação prática no projeto eletrônico.
Circuito da série RC
Um circuito da série RC, essencialmente composto por um resistor (R) e um capacitor (C) Em série, opera com um princípio simples.Quando o interruptor do circuito é fechado, o capacitor começa a cobrar da tensão aplicada (V), iniciando um fluxo de corrente através do circuito.À medida que o capacitor cobra, a corrente aumenta gradualmente até que o capacitor atinja sua capacidade, momento em que para de aceitar a carga, e a atual se estabiliza pelo seu valor máximo, calculado como 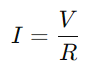 .
.
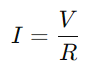 .
.O processo de carregamento do capacitor pode ser descrito matematicamente pela equação 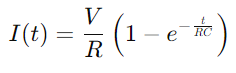 , onde eu é a corrente, V é a tensão, R é a resistência, C é a capacitância, t é hora e e é a base do logaritmo natural.Essa fórmula reflete como a corrente muda ao longo do tempo, à medida que o capacitor cobra, com o produto dos valores de resistência e capacitância (RC) definindo a constante de tempo do circuito, indicativo da velocidade com que o capacitor cobra.
, onde eu é a corrente, V é a tensão, R é a resistência, C é a capacitância, t é hora e e é a base do logaritmo natural.Essa fórmula reflete como a corrente muda ao longo do tempo, à medida que o capacitor cobra, com o produto dos valores de resistência e capacitância (RC) definindo a constante de tempo do circuito, indicativo da velocidade com que o capacitor cobra.
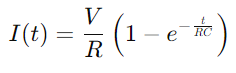 , onde eu é a corrente, V é a tensão, R é a resistência, C é a capacitância, t é hora e e é a base do logaritmo natural.Essa fórmula reflete como a corrente muda ao longo do tempo, à medida que o capacitor cobra, com o produto dos valores de resistência e capacitância (RC) definindo a constante de tempo do circuito, indicativo da velocidade com que o capacitor cobra.
, onde eu é a corrente, V é a tensão, R é a resistência, C é a capacitância, t é hora e e é a base do logaritmo natural.Essa fórmula reflete como a corrente muda ao longo do tempo, à medida que o capacitor cobra, com o produto dos valores de resistência e capacitância (RC) definindo a constante de tempo do circuito, indicativo da velocidade com que o capacitor cobra.
Figura 2: Circuito da série RC
A descarga ocorre quando o interruptor é aberto, revertendo o processo: a energia armazenada no capacitor é liberada, fazendo com que a corrente flua na direção oposta até que o capacitor seja drenado.Esse ciclo de carregamento e descarga é crucial em aplicações como conversão de sinal, filtragem e circuitos de tempo devido à maneira previsível pela qual a mudança de corrente e tensão.

Figura 3: curto -circuito da série RC
O comportamento do circuito da série RC também varia com a frequência.Em baixas frequências, o capacitor age mais como um circuito aberto, impedindo bastante o fluxo de corrente.À medida que a frequência aumenta, a reatância capacitiva diminui, facilitando a passagem da corrente.Essa mudança na impedância com a frequência permite que o circuito da série RC atue como um filtro, atenuando seletivamente as frequências abaixo de um determinado limite (frequência de girar 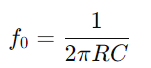 ).
).
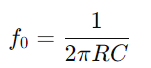 ).
).
Figura 4: Carregamento e descarga dos circuitos da série RC
Além das operações em estado estacionário, os circuitos RC também são estudados para suas respostas transitórias quando submetidas a alterações repentinas na tensão, como quando uma fonte de alimentação CC é ligada ou desativada.Esse cenário é denominado um processo transitório, onde o circuito transita de um estado estável para outro.A dinâmica desse processo depende significativamente da constante de tempo RC, que governa a rapidez com que o circuito reage às mudanças.
Por fim, os circuitos da série RC servem várias funções em aplicativos CC e CA, manipulando tarefas que variam de atrasar sinais à integração ou acoplamento de vários elementos de circuito.Essa versatilidade decorre das interações exclusivas entre o resistor e o capacitor, que juntos determinam a resposta geral do circuito a alterações na tensão e frequência.

Figura 5: Diagrama de circuito da série RC e fórmula de frequência
Em um circuito da série RC, a interação entre o resistor (R) e o capacitor (C) influencia a distribuição atual do fluxo e da tensão.O papel principal do resistor é regular o fluxo atual.Este relacionamento é quantificado pela lei de Ohm, que afirma 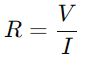 , onde V é tensão e EU é atual.Essencialmente, o resistor atua como um gargalo, controlando quanta eletricidade pode passar a qualquer momento.
, onde V é tensão e EU é atual.Essencialmente, o resistor atua como um gargalo, controlando quanta eletricidade pode passar a qualquer momento.
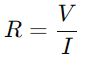 , onde V é tensão e EU é atual.Essencialmente, o resistor atua como um gargalo, controlando quanta eletricidade pode passar a qualquer momento.
, onde V é tensão e EU é atual.Essencialmente, o resistor atua como um gargalo, controlando quanta eletricidade pode passar a qualquer momento.A função do capacitor é um pouco mais complexa, pois armazena temporariamente a energia elétrica e a libera de volta ao circuito.A tensão através do capacitor (Vc) correlaciona -se com sua carga armazenada (Q) e é calculado usando a fórmula 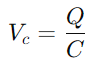 .Esse relacionamento destaca a capacidade do capacitor de manter o custo, impactando diretamente a tensão que ele exibe.Durante a operação, a dinâmica de cobrança e descarregamento do capacitor é vital para a compreensão dos circuitos RC.O tempo constante (τ), definido como
.Esse relacionamento destaca a capacidade do capacitor de manter o custo, impactando diretamente a tensão que ele exibe.Durante a operação, a dinâmica de cobrança e descarregamento do capacitor é vital para a compreensão dos circuitos RC.O tempo constante (τ), definido como 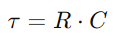 , mede a rapidez com que o capacitor atinge aproximadamente 63,2% da tensão completa fornecida pela fonte (V0).Essa constante de tempo é indicativa de como o circuito se adapta às alterações de entrada, com as propriedades do resistor e do capacitor ditando o ritmo desses ajustes.
, mede a rapidez com que o capacitor atinge aproximadamente 63,2% da tensão completa fornecida pela fonte (V0).Essa constante de tempo é indicativa de como o circuito se adapta às alterações de entrada, com as propriedades do resistor e do capacitor ditando o ritmo desses ajustes.
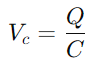 .Esse relacionamento destaca a capacidade do capacitor de manter o custo, impactando diretamente a tensão que ele exibe.Durante a operação, a dinâmica de cobrança e descarregamento do capacitor é vital para a compreensão dos circuitos RC.O tempo constante (τ), definido como
.Esse relacionamento destaca a capacidade do capacitor de manter o custo, impactando diretamente a tensão que ele exibe.Durante a operação, a dinâmica de cobrança e descarregamento do capacitor é vital para a compreensão dos circuitos RC.O tempo constante (τ), definido como 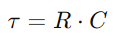 , mede a rapidez com que o capacitor atinge aproximadamente 63,2% da tensão completa fornecida pela fonte (V0).Essa constante de tempo é indicativa de como o circuito se adapta às alterações de entrada, com as propriedades do resistor e do capacitor ditando o ritmo desses ajustes.
, mede a rapidez com que o capacitor atinge aproximadamente 63,2% da tensão completa fornecida pela fonte (V0).Essa constante de tempo é indicativa de como o circuito se adapta às alterações de entrada, com as propriedades do resistor e do capacitor ditando o ritmo desses ajustes.A tensão em todo o capacitor a qualquer momento durante a cobrança é dada por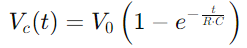 , ilustrando um aumento não linear à medida que o capacitor preenche.Esta equação descreve como a taxa de carga diminui à medida que o capacitor se aproxima da capacidade total.
, ilustrando um aumento não linear à medida que o capacitor preenche.Esta equação descreve como a taxa de carga diminui à medida que o capacitor se aproxima da capacidade total.
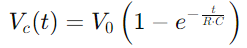 , ilustrando um aumento não linear à medida que o capacitor preenche.Esta equação descreve como a taxa de carga diminui à medida que o capacitor se aproxima da capacidade total.
, ilustrando um aumento não linear à medida que o capacitor preenche.Esta equação descreve como a taxa de carga diminui à medida que o capacitor se aproxima da capacidade total.Por outro lado, durante a alta, a tensão do capacitor diminui de acordo com 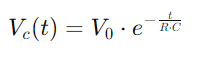 , retratando uma diminuição linear na energia armazenada ao longo do tempo.Esse processo fornece uma imagem clara de como a energia é liberada do capacitor de volta ao circuito.Em aplicações de CA, a diferença de fase entre a tensão e a corrente, φ, torna -se crítico.Essa diferença, calculada como
, retratando uma diminuição linear na energia armazenada ao longo do tempo.Esse processo fornece uma imagem clara de como a energia é liberada do capacitor de volta ao circuito.Em aplicações de CA, a diferença de fase entre a tensão e a corrente, φ, torna -se crítico.Essa diferença, calculada como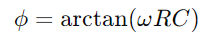 onde ω Representa a frequência angular, mostra o atraso causado pelo capacitor, que afeta o tempo entre quando os fluxos de corrente e a tensão mudam nos componentes.
onde ω Representa a frequência angular, mostra o atraso causado pelo capacitor, que afeta o tempo entre quando os fluxos de corrente e a tensão mudam nos componentes.
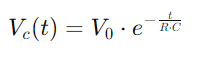 , retratando uma diminuição linear na energia armazenada ao longo do tempo.Esse processo fornece uma imagem clara de como a energia é liberada do capacitor de volta ao circuito.Em aplicações de CA, a diferença de fase entre a tensão e a corrente, φ, torna -se crítico.Essa diferença, calculada como
, retratando uma diminuição linear na energia armazenada ao longo do tempo.Esse processo fornece uma imagem clara de como a energia é liberada do capacitor de volta ao circuito.Em aplicações de CA, a diferença de fase entre a tensão e a corrente, φ, torna -se crítico.Essa diferença, calculada como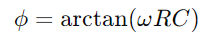 onde ω Representa a frequência angular, mostra o atraso causado pelo capacitor, que afeta o tempo entre quando os fluxos de corrente e a tensão mudam nos componentes.
onde ω Representa a frequência angular, mostra o atraso causado pelo capacitor, que afeta o tempo entre quando os fluxos de corrente e a tensão mudam nos componentes.No geral, o resistor limita e direciona o fluxo de corrente enquanto o capacitor armazena e modula a tensão.Juntos, eles determinam as características de resposta do circuito, como a rapidez com que ele pode carregar e descarregar e as mudanças de fase que ocorrem nos cenários atuais alternados.Esse comportamento combinado sustenta as operações fundamentais dos circuitos da série RC, tornando -os integrantes em várias aplicações eletrônicas.
Equações básicas do circuito da série RC
Para entender o comportamento de um circuito da série RC, é crucial começar com as equações básicas que descrevem sua resposta a alterações na tensão de entrada.Suponha que tenhamos uma tensão de entrada em mudança representada como Vin (T), com a tensão em todo o resistor rotulado como VR (T) e em todo o capacitor como VC (T).Em um circuito em série, a mesma corrente, Isto) flui através do resistor e do capacitor.
Aplicando a lei de tensão de Kirchhoff (KVL), que afirma que a tensão total em torno de qualquer circuito fechado em um circuito deve ser igual a zero, descobrimos que a tensão de entrada é igual à soma das tensões através do resistor e do capacitor:

A tensão em todo o resistor pode ser calculada usando a lei de Ohm:
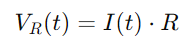
Para o capacitor, a tensão VC (t) está relacionada à cobrança q (t) que é dada por:
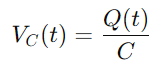
Como a corrente é definida como a taxa de fluxo de carga, temos:
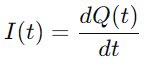
Substituindo Q (t) na equação para VC (T)e usando o derivado de carga Isto), derivamos a equação diferencial do núcleo para o circuito da série RC:

Substituindo ainda mais Q (t) com a integral de Isto), nós conseguimos:
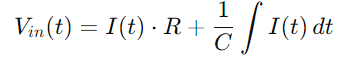
Para o atual i (t), considerando a taxa de mudança de tensão em todo o capacitor, usamos:
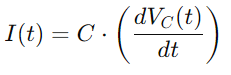
A integração de todos esses relacionamentos nos dá a equação diferencial que descreve a tensão em todo o capacitor:
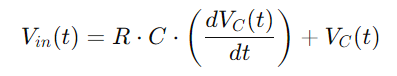
Esta é uma equação diferencial linear de primeira ordem que captura a mudança de tensão dependente do tempo em todo o capacitor.A solução dessa equação nos permite descrever com precisão como a tensão do capacitor evolui.Esse entendimento é fundamental para analisar os ciclos de carregamento e descarga do capacitor, bem como a resposta do circuito a diferentes frequências.Essa abordagem abrangente fornece uma visão profunda das características dinâmicas do circuito da série RC.

Figura 6: Equação diferencial de tensão
Impedância do circuito da série RC
Para reescrever a descrição de um circuito da série RC, com foco na interação humana e uma explicação direta e simplificada, vamos aprimorar as experiências tangíveis e operações passo a passo envolvidas, mantendo a mensagem principal e a coerência:
Em um circuito da série RC, o resistor e o capacitor trabalham em conjunto para controlar o fluxo de eletricidade, crucial ao lidar com correntes alternadas.A impedância total do circuito, representada como 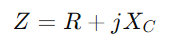 , combina a resistência r e a reatância capacitiva XC.O principal recurso dessa configuração é que os valores de impedância para ambos os componentes variam com as alterações de frequência.À medida que a frequência aumenta, a impedância do capacitor diminui, permitindo que mais corrente passasse, enquanto a resistência permanece essencialmente constante.
, combina a resistência r e a reatância capacitiva XC.O principal recurso dessa configuração é que os valores de impedância para ambos os componentes variam com as alterações de frequência.À medida que a frequência aumenta, a impedância do capacitor diminui, permitindo que mais corrente passasse, enquanto a resistência permanece essencialmente constante.
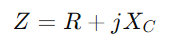 , combina a resistência r e a reatância capacitiva XC.O principal recurso dessa configuração é que os valores de impedância para ambos os componentes variam com as alterações de frequência.À medida que a frequência aumenta, a impedância do capacitor diminui, permitindo que mais corrente passasse, enquanto a resistência permanece essencialmente constante.
, combina a resistência r e a reatância capacitiva XC.O principal recurso dessa configuração é que os valores de impedância para ambos os componentes variam com as alterações de frequência.À medida que a frequência aumenta, a impedância do capacitor diminui, permitindo que mais corrente passasse, enquanto a resistência permanece essencialmente constante.A impedância, indicada como Z e medido em ohms (Ω), desempenha um papel crítico na determinação de como o circuito reage à corrente alternada.Como nos circuitos da série RL, a resistência R e reatância capacitiva xC de um circuito RC forma um triângulo conhecido como triângulo de impedância.Este triângulo está intimamente relacionado ao triângulo de tensão e, ao aplicar o teorema do pitagoroso, você pode calcular a impedância total do circuito.

Figura 7: Fórmula de cálculo do circuito da série RC
Quando se trata de aplicações práticas, considere os fones de ouvido, que usam esses princípios.Os fones de ouvido de alta impedância, geralmente superiores a 200 ohms, são normalmente usados com computadores de mesa, amplificadores de energia e equipamentos de áudio profissional.Esses modelos de alta impedância correspondem bem aos recursos de saída dos eletrônicos de nível profissional.Ao usar esses fones de ouvido, é crucial ajustar o volume gradualmente para evitar a sobrecarga e danificar os delicados componentes internos, como a bobina de voz.
Por outro lado, fones de ouvido de baixa impedância, geralmente abaixo de 50 ohms, são preferidos a dispositivos portáteis, como CD players, MD Players ou MP3 Players.Esses fones de ouvido exigem menos energia para fornecer áudio de alta qualidade, tornando-os ideais para uso móvel.No entanto, eles também exigem atenção cuidadosa aos níveis de sensibilidade para garantir o desempenho ideal e evitar danos aos fones de ouvido ou audição.

Figura 8: Diagrama de impedância do circuito da série RC
Procedimentos de admissão e análise dos circuitos da série RC
A admissão mede a facilidade com que um circuito da série RC pode conduzir eletricidade, calculada como o inverso da impedância ( ).Este valor integra a resistência (R) e a reatância (X) do circuito.A resistência se opõe ao fluxo de corrente convertendo energia elétrica em calor, enquanto a reatância armazena energia temporariamente no circuito.
).Este valor integra a resistência (R) e a reatância (X) do circuito.A resistência se opõe ao fluxo de corrente convertendo energia elétrica em calor, enquanto a reatância armazena energia temporariamente no circuito.
 ).Este valor integra a resistência (R) e a reatância (X) do circuito.A resistência se opõe ao fluxo de corrente convertendo energia elétrica em calor, enquanto a reatância armazena energia temporariamente no circuito.
).Este valor integra a resistência (R) e a reatância (X) do circuito.A resistência se opõe ao fluxo de corrente convertendo energia elétrica em calor, enquanto a reatância armazena energia temporariamente no circuito.Para calcular a admissão
Comece escrevendo a impedância 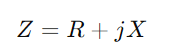 , onde R significa resistência, X para reatância, e j é a unidade imaginária.Use a fórmula y = 1/(R + jx).Esta operação envolve números complexos e nos dá
, onde R significa resistência, X para reatância, e j é a unidade imaginária.Use a fórmula y = 1/(R + jx).Esta operação envolve números complexos e nos dá 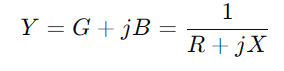 .Aqui, G é a condutância (capacidade de fluxo atual real) e B é a suscetância (a capacidade do circuito de reagir às mudanças na corrente).
.Aqui, G é a condutância (capacidade de fluxo atual real) e B é a suscetância (a capacidade do circuito de reagir às mudanças na corrente).
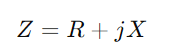 , onde R significa resistência, X para reatância, e j é a unidade imaginária.Use a fórmula y = 1/(R + jx).Esta operação envolve números complexos e nos dá
, onde R significa resistência, X para reatância, e j é a unidade imaginária.Use a fórmula y = 1/(R + jx).Esta operação envolve números complexos e nos dá 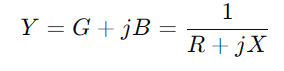 .Aqui, G é a condutância (capacidade de fluxo atual real) e B é a suscetância (a capacidade do circuito de reagir às mudanças na corrente).
.Aqui, G é a condutância (capacidade de fluxo atual real) e B é a suscetância (a capacidade do circuito de reagir às mudanças na corrente).
Figura 9: Calculadora de impedância de circuito da série RC
Esse cálculo revela não apenas a condutividade do circuito, mas também suas características de resposta dinâmica, cruciais para análise do circuito CA.A condutância e a suscetância, tomadas em conjunto, indicam como o circuito passa por corrente e como ele armazena e libera energia.

Figura 10: fórmula do ângulo de fase
Aplicação prática
Os engenheiros usam valores de admissão para aprimorar o design do circuito, especialmente em aplicações de alta frequência, como circuitos de radiofrequência.O ajuste da admissão ajuda na correspondência de impedância, reduzindo a reflexão do sinal e aumentando a eficiência da transmissão.
Ao estudar a resposta da admissão, os engenheiros podem avaliar e prever o desempenho do circuito sob várias condições, como resposta de frequência, estabilidade e sensibilidade.Equipe com um osciloscópio e um gerador de sinal para medir a tensão e a corrente do circuito em frequências variadas.Concentre -se especialmente na frequência de corte para testar previsões teóricas e validá -las contra observações práticas.Para circuitos CA, comece determinando a reatância (XC) do capacitor com 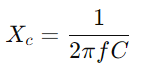 , onde f é a frequência do sinal.Calcular a impedância total
, onde f é a frequência do sinal.Calcular a impedância total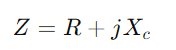 e então admissão
e então admissão  .
.
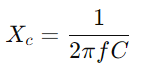 , onde f é a frequência do sinal.Calcular a impedância total
, onde f é a frequência do sinal.Calcular a impedância total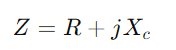 e então admissão
e então admissão  .
.Analise a diferença de fase usando 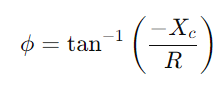 Para entender a alteração da forma do sinal.Examine como o circuito lida com diferentes frequências, principalmente observando o comportamento na frequência de corte
Para entender a alteração da forma do sinal.Examine como o circuito lida com diferentes frequências, principalmente observando o comportamento na frequência de corte 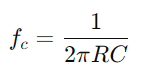 , onde o circuito muda de passagem para sinais de bloqueio.Avaliar como a impedância e a diferença de fase variam com a frequência, é crucial para projetar filtros e processadores de sinal eficazes.Discuta como a seletividade da frequência, as mudanças de fase e a atenuação do sinal devido às propriedades do circuito afetam aplicações práticas como filtragem e ajuste eletrônico.
, onde o circuito muda de passagem para sinais de bloqueio.Avaliar como a impedância e a diferença de fase variam com a frequência, é crucial para projetar filtros e processadores de sinal eficazes.Discuta como a seletividade da frequência, as mudanças de fase e a atenuação do sinal devido às propriedades do circuito afetam aplicações práticas como filtragem e ajuste eletrônico.
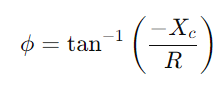 Para entender a alteração da forma do sinal.Examine como o circuito lida com diferentes frequências, principalmente observando o comportamento na frequência de corte
Para entender a alteração da forma do sinal.Examine como o circuito lida com diferentes frequências, principalmente observando o comportamento na frequência de corte 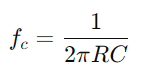 , onde o circuito muda de passagem para sinais de bloqueio.Avaliar como a impedância e a diferença de fase variam com a frequência, é crucial para projetar filtros e processadores de sinal eficazes.Discuta como a seletividade da frequência, as mudanças de fase e a atenuação do sinal devido às propriedades do circuito afetam aplicações práticas como filtragem e ajuste eletrônico.
, onde o circuito muda de passagem para sinais de bloqueio.Avaliar como a impedância e a diferença de fase variam com a frequência, é crucial para projetar filtros e processadores de sinal eficazes.Discuta como a seletividade da frequência, as mudanças de fase e a atenuação do sinal devido às propriedades do circuito afetam aplicações práticas como filtragem e ajuste eletrônico.Essa abordagem divide os processos operacionais em etapas gerenciáveis, enriquecendo o entendimento do usuário com informações práticas sobre o manuseio e analisando os circuitos da série RC.

Figura 11: Características dos circuitos da série RC
Diagrama de fasores do circuito da série RC
Em um circuito da série RC, todos os elementos compartilham a mesma corrente devido à configuração da série.Essa corrente uniforme atua como uma linha de base para o nosso diagrama de fasoros, o que ajuda a visualizar a relação entre diferentes tensões e correntes no circuito.Vamos designar esta corrente EU como fasor de referência, posicionado a zero graus no diagrama.No diagrama, a corrente EU está definido horizontalmente à direita, estabelecendo a linha de referência zero grau.A tensão através do resistor (UR) está em fase com a corrente porque os resistores não causam nenhuma mudança de fase.Por isso, UR é desenhado como um vetor horizontal na mesma direção que EU, estendendo -se da origem.

Figura 12: Diagrama de fasores de circuito da série RC
Por outro lado, a tensão em todo o capacitor (UC) leva a corrente em 90 graus devido à propriedade capacitiva de atrasar a fase atual.Esta tensão é representada por um vetor vertical apontando para cima, começando pela ponta do UR vetor.A tensão total U no circuito está a soma vetorial de U Rand UC.Esta soma forma um triângulo certo com UR e UC como lados adjacentes e opostos, respectivamente.A hipotenusa deste triângulo, estendendo -se da origem até a ponta do UC vetor, representa U.
A corrente sinusoidal através do circuito é dada pelo pecado (ωt), onde IM é a amplitude da corrente máxima e ω é a frequência angular.Consequentemente, a tensão em todo o resistor é  , espelhando a forma de onda atual.A tensão em todo o capacitor é dada por
, espelhando a forma de onda atual.A tensão em todo o capacitor é dada por 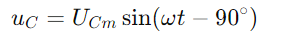 , indicando uma mudança de fase de -90 ° (ou 90 graus à frente da corrente).O triângulo certo do diagrama de fasores esclarece que
, indicando uma mudança de fase de -90 ° (ou 90 graus à frente da corrente).O triângulo certo do diagrama de fasores esclarece que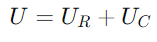 não está apenas em magnitude, mas também em relação de fase, com o vetor de tensão terminal (U) completando o triângulo.
não está apenas em magnitude, mas também em relação de fase, com o vetor de tensão terminal (U) completando o triângulo.
 , espelhando a forma de onda atual.A tensão em todo o capacitor é dada por
, espelhando a forma de onda atual.A tensão em todo o capacitor é dada por 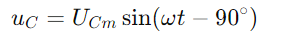 , indicando uma mudança de fase de -90 ° (ou 90 graus à frente da corrente).O triângulo certo do diagrama de fasores esclarece que
, indicando uma mudança de fase de -90 ° (ou 90 graus à frente da corrente).O triângulo certo do diagrama de fasores esclarece que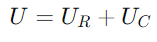 não está apenas em magnitude, mas também em relação de fase, com o vetor de tensão terminal (U) completando o triângulo.
não está apenas em magnitude, mas também em relação de fase, com o vetor de tensão terminal (U) completando o triângulo.
Figura 13: Diagrama de fasores de tensão do circuito da série RC
Pontos -chave na análise dos circuitos da série RC
Impedância no circuito da série RC, representado como Z, combina resistência (R) e o efeito reativo da capacitância em uma única medida que varia com a frequência do sinal.É expresso matematicamente como 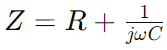 , onde ω é a frequência angular e C é a capacitância.Aqui, R constitui a parte real da impedância e
, onde ω é a frequência angular e C é a capacitância.Aqui, R constitui a parte real da impedância e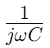 Representa a parte imaginária, indicando como o capacitor influencia o circuito.
Representa a parte imaginária, indicando como o capacitor influencia o circuito.
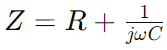 , onde ω é a frequência angular e C é a capacitância.Aqui, R constitui a parte real da impedância e
, onde ω é a frequência angular e C é a capacitância.Aqui, R constitui a parte real da impedância e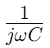 Representa a parte imaginária, indicando como o capacitor influencia o circuito.
Representa a parte imaginária, indicando como o capacitor influencia o circuito.A maneira como a impedância muda com a frequência é fundamental para o uso de circuitos RC em série em aplicações de filtragem.Em frequências mais baixas, o circuito exibe maior impedância, bloqueando efetivamente essas frequências.Por outro lado, em frequências mais altas, a impedância cai, permitindo que essas frequências passassem mais livremente.Esse comportamento torna os circuitos RC da série ideais para tarefas como filtrar ruído indesejado de baixa frequência ou passar sinais de alta frequência.

Figura 14: Diagrama vetorial de impedância do circuito da série RC
Conclusão
Desde a filtragem de frequências indesejadas até as respostas dos sinais de modelagem, o circuito da série RC é fundamental em uma ampla gama de funções eletrônicas.Ao entender os princípios subjacentes, como impedância, relações de fasoros e o comportamento dependente da frequência desses circuitos, engenheiros e designers estão equipados para criar soluções que gerenciem efetivamente a integridade do sinal em sistemas eletrônicos complexos.O exame detalhado desses circuitos, apoiado por análises matemáticas e representações visuais, como diagramas de fasores, oferece uma visão abrangente que é importante para quem deseja aprofundar sua compreensão da dinâmica eletrônica de circuitos ou aprimorar suas habilidades práticas no design de circuitos e solução de problemas.
Perguntas frequentes [FAQ]
1. Qual é o princípio do circuito RC?
O princípio de um circuito RC (capacitor de resistor) gira em torno dos processos de carregamento e descarga do capacitor através do resistor.Nesse circuito, a capacidade do capacitor de armazenar e liberar energia elétrica interage com o resistor, que controla a taxa na qual o capacitor cobra ou descarrega.
2. Por que um circuito RC circunda a corrente?
Em um circuito RC, a corrente leva a tensão no capacitor porque o capacitor precisa começar a carregar antes que sua tensão possa aumentar.Como a corrente flui para o capacitor para carregá -lo, os picos de corrente antes da tensão no capacitor atingirem seu máximo.Esse efeito causa uma mudança de fase, onde a fase atual leva a fase de tensão em até 90 graus, dependendo da frequência do sinal de entrada.
3. Como a tensão muda em um circuito RC?
A mudança de tensão em um circuito RC durante o carregamento é descrita por uma função exponencial.Quando uma tensão é aplicada, a tensão no capacitor aumenta inicialmente rapidamente, depois diminui a velocidade à medida que se aproxima da tensão de alimentação.Matematicamente, isso é expresso como 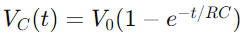 , onde VC(t) é a tensão no capacitor no tempo t, v0 é a tensão de alimentação e o RC é a constante de tempo do circuito, determinando a rapidez com que o capacitor cobra.Por outro lado, durante a descarga, a tensão em todo o capacitor diminui exponencialmente, seguindo a equação
, onde VC(t) é a tensão no capacitor no tempo t, v0 é a tensão de alimentação e o RC é a constante de tempo do circuito, determinando a rapidez com que o capacitor cobra.Por outro lado, durante a descarga, a tensão em todo o capacitor diminui exponencialmente, seguindo a equação 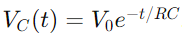 .
.
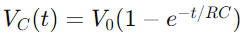 , onde VC(t) é a tensão no capacitor no tempo t, v0 é a tensão de alimentação e o RC é a constante de tempo do circuito, determinando a rapidez com que o capacitor cobra.Por outro lado, durante a descarga, a tensão em todo o capacitor diminui exponencialmente, seguindo a equação
, onde VC(t) é a tensão no capacitor no tempo t, v0 é a tensão de alimentação e o RC é a constante de tempo do circuito, determinando a rapidez com que o capacitor cobra.Por outro lado, durante a descarga, a tensão em todo o capacitor diminui exponencialmente, seguindo a equação 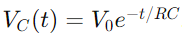 .
. SOBRE NóS
Satisfação do cliente sempre.Confiança mútua e interesses comuns.
SOBRE NóS
Satisfação do cliente sempre.Confiança mútua e interesses comuns.
teste de funcionamento.Os produtos mais econômicos e o melhor serviço é o nosso compromisso eterno.
Artigo quente
- São CR2032 e CR2016
- MOSFET: definição, princípio de trabalho e seleção
- Instalação e teste de relé, interpretação dos diagramas de fiação de relé
- CR2016 vs. CR2032 Qual é a diferença
- NPN vs. PNP: Qual é a diferença?
- Esp32 vs STM32: Qual microcontrolador é melhor para você?
- LM358 GUIA AMPLIFENCIADOR OPERACIONAL DO DULO
- CR2032 VS DL2032 VS CR2025 Guia de comparação
- Compreendendo as diferenças ESP32 e ESP32-S3 Análise técnica e de desempenho
- Análise detalhada do circuito da série RC
 Análise aprofundada de diodos 1N4148: modos de operação, especificações e cenários de uso
Análise aprofundada de diodos 1N4148: modos de operação, especificações e cenários de uso
2024-05-08
 Compreendendo os tipos e usos de bombas de deslocamento dinâmico e positivo
Compreendendo os tipos e usos de bombas de deslocamento dinâmico e positivo
2024-05-07
Número da peça quente
 CX0603MRX7R9BB103
CX0603MRX7R9BB103 1206AC472KAZ1A
1206AC472KAZ1A 08055A5R0CAT2A
08055A5R0CAT2A CGA3E2X8R2A153M080AD
CGA3E2X8R2A153M080AD 0201ZA150JAT2A
0201ZA150JAT2A 12061A910GAT2A
12061A910GAT2A 12105G105ZAT2A
12105G105ZAT2A UMK105CG2R2CW-F
UMK105CG2R2CW-F T495D686M020ATE150
T495D686M020ATE150 SIR622DP-T1-GE3
SIR622DP-T1-GE3
- HSMS-2860-BLKG
- TC58NYG0S3HBAI6
- EPF10K130EBC600-1
- A3938SLD
- HCPL-070A-500E
- 742792625
- MEF1S0505SP3C
- VE-J54-EZ
- VE-JW3-IZ
- TL16C752CIPFBR
- F971A106MBAHT3
- OPA548TG3
- BQ2060A-E619DBQRG4
- SN74LVCR2245AZQNR
- LTM8046IY#PBF
- LP2975IMM-3.3/NOPB
- ST62T25CM6/TR
- TLK10021ZWQ
- INA210AIDCKT
- XC7K325T-1FF900I
- FAN2558S12X
- XCV300-4BG352C
- TPS77318DGKR
- T491B106K010ZGPV10ZB01
- ACPL-W341
- AM29F400BB-90SC
- BCM5802KQM
- CSD58887Q3
- HMC485GETR
- ICS1562AM
- RF4E110BN
- M82352G-12
- GM5120-BD
- HM5112805FTD-5
- PMB2906EV1.2B
- T8K26EXBG-0
- LTM4622EY
- MC33PF8100EQES
- ME3220-472MLB